Uno dei punti di svolta fondamentali nel corso dell’evoluzione del genere umano è rappresentato dall’invenzione del denaro. Molti animali, infatti, conducono una vita da individui, senza mai costruire una società (pensiamo, per esempio, ai gatti). Altri animali, ma in numero inferiore, hanno imparato a vivere in società più o meno grandi: molte scimmie vivono in vere e proprie famiglie, più o meno organizzate. Ed è naturale che, quando c’è una organizzazione sociale in un gruppo, ogni individuo abbia un compito che serve alla comunità. L’individuo cede qualcosa al gruppo, ed il gruppo ridistribuisce i beni a tutti gli individui. Nasce quindi l’esigenza del baratto: una scimmia raccoglie delle banane, ed un’altra raccoglie dei mango. La prima consegnerà un paio di banane alla seconda in cambio di un frutto di mango, e viceversa. Il baratto, dunque, è una componente fondamentale della società, perché grazie ad esso non è necessario che tutti sappiano fare tutto e ci si può specializzare in un compito particolare sapendo che qualcun altro si occuperà del resto. Gli animali che hanno implementato un modello di società tendono a seguire il meccanismo del baratto. Ma solo un animale è, finora, riuscito a superare il baratto con un trucco: fissare in modo univoco il valore di un certo oggetto. È il concetto di denaro, e l’animale in questione è ovviamente l’uomo. L’acquisto di beni o servizi tramite denaro è, fondamentalmente, una forma di baratto: il cliente prende dal venditore un casco di banane in cambio di un pezzo di metallo che, per convenzione, vale 2 euro. Ma l’uso del denaro ha due vantaggi importantissimi rispetto al baratto: il primo vantaggio è che in questo modo è più facile tenere sotto controllo il valore delle cose. Infatti, un venditore può barattare un caso di banane con un ananas, mentre un altro venditore baratta lo stesso casco di banane con una capra. Ma difficilmente si potrebbe vendere quel casco di banane per 2 euro in un negozio e 20 euro nell’altro. L’altro grande vantaggio è la possibilità di accumulare il denaro per tempi migliori: non si possono accumulare banane per aspettare di barattarle con qualcos’altro durante l’inverno o addirittura negli anni a venire, perché marcirebbero nel frattempo. Invece, nel caso del denaro, è possibile metterlo da parte per spenderlo in momenti di magra. È il concetto delle pensioni: durante la vita lavorativa si mettono da parte dei soldi, che vengono poi utilizzati per mantenersi quando non si è più in grado di lavorare. E se già così non ci piace molto l’idea di mettere da parte denaro per almeno vent’anni, mettere da parte banane e ananas per due decadi avrebbe risultati decisamente peggiori.

I “bug” del denaro

L’introduzione che avete appena letto è, probabilmente, inutile: tutti noi utilizziamo denaro ogni giorno. Ma, proprio perché ne siamo tanto abituati, lo diamo per scontato non pensiamo troppo a come funzioni davvero il meccanismo dell’acquisto, in contrapposizione a quello del baratto.
Ora la domanda è: quali sono le vulnerabilità del denaro? Sicuramente, la contraffazione: fin da quando è apparso per la prima volta, il denaro è stato soggetto a falsificazioni. I progettisti delle varie monete hanno sempre cercato, nel corso dei secoli, metodi per rendere la vita più difficile possibile ai falsari. Nel corso degli ultimi secoli si sono utilizzate monete realizzate con punzoni particolari, difficili da replicare fedelmente, mentre oggi siamo abituati a vedere sulle banconote filigrane molto particolari. Ma i falsari prima o poi riescono sempre a trovare un metodo per duplicare il denaro.
L’avvento della contabilità digitale ha in buona parte risolto questo problema, ma ne ha introdotto un altro: la tracciabilità, che può generare nella violazione della privacy.
C’è una precisazione da fare: abbiamo parlato di “contabilità digitale” e non di “denaro digitale”. Infatti, quando facciamo un acquisto online tramite Visa o Mastercard, il denaro è sempre reale: la contabilità delle transazioni è digitale. In pratica, non cambia il meccanismo di pagamento: alla fin fine se acquistiamo una penna su ebay, il denaro che paghiamo arriverà in mano al venditore. Possiamo schematizzare in questo modo: noi versiamo dei contanti alla nostra banca, la somma entra nel nostro conto corrente online, paghiamo la cifra dovuta al commerciante, tale cifra viene spostata sul conto del venditore, e questo va alla sede della sua banca per prelevare, tramite bancomat, il denaro. I denaro rimane sempre sotto forma di monete o banconote, anche se le banconote che il venditore si ritroverà in mano non saranno fisicamente le stesse che noi avevamo versato in banca. Il denaro in circolo è sempre rappresentato da banconote fisiche.
Quello che cambia è il modo in cui le transazioni vengono registrate: con la contabilità “classica” è facile perdere le tracce dopo un paio di intermediari. Per esempio, se acquistiamo un ombrello pagando in banconote innanzitutto non è possibile sapere che siamo stati davvero noi ad eseguire l’acquisto e non, piuttosto, qualcun altro. In secondo luogo, il commerciante avrà segnato la cifra che gli abbiamo corrisposto tra le sue entrate, ma a sua volta è difficile capire (anche se non impossibile) quale parte del denaro che gli abbiamo corrisposto rappresenta davvero il valore dell’ombrello e quale parte, invece, è il guadagno personale del commerciante che nulla ha a che vedere con il valore dell’oggetto in se.
Riassumendo, il problema sta nel fatto che gli acquisti sono facilmente tracciabili, e questo può rivelarsi un problema soprattutto in paesi privi delle libertà fondamentali. Un dissidente di un regime autoritario ha sicuramente il conto corrente sotto controllo.
Inoltre, il sistema è centralizzato, e i gestori possono commettere violazioni sui correntisti: l’esempio più noto è quello di Julian Assange, che dopo avere messo in imbarazzo il governo degli Stati Uniti si è ritrovato con i conti correnti congelati, impossibilitato ad eseguire qualsiasi pagamento, senza che vi fosse un provvedimento del tribunale ma per spontanea decisione degli istituti bancari.

La soluzione

Dunque, il denaro “analogico” ha due punti deboli: la falsificazione e la tracciabilità, e l’entità dei problemi varia a seconda del fatto che si usi una contabilità “tradizionale” oppure “digitale”. Qualcuno, però, ha pensato ad un modo per risolvere queste vulnerabilità: passare completamente al digitale. Il programmatore Satoshi Nakamoto (è uno pseudonimo, non si conosce il nome reale di questa persona) ha proposto, nel 2008, una idea di cryptocurrency, cioè di “moneta virtuale cifrata”. Il concetto stesso di cryptocurrency era già stato suggerito nel 1998, ma nessuno aveva mai realizzato prima una implementazione ben funzionante come quella di Satoshi Nakamoto, conosciuta col nome di Bitcoin.

Come funziona una moneta digitale? Abbiamo visto che una moneta è in realtà un qualsiasi oggetto a cui viene dato un valore preciso, e che viene scambiata con altri oggetti come in una sorta di baratto. Quindi, per realizzare una moneta virtuale potremmo utilizzare un qualsiasi oggetto digitale, ed assegnargli un valore: una immagine, un file audio, una stringa di testo. Naturalmente, questi esempi non vanno bene, perché sono troppo facili da replicare: è necessario qualcosa di univoco, cioè una tipologia di oggetto in cui ogni esemplare è riconoscibile e non duplicabile (un meccanismo, quindi, simile a quello dei numeri di serie sulle banconote). La matematica ci viene in aiuto, ed ecco quindi il concetto di cryptocurrency. L’idea è di utilizzare particolari funzioni matematiche che consentono di calcolare coppie di numeri tra essi collegati ma tali da non poter risalire ad uno dei due anche se si conosce l’altro, di modo che l’unico a conoscerli entrambe sia chi li ha calcolati. È la stessa logica della crittografia asimmetrica.

Rivest, Shamir, Adleman

Tutti noi abbiamo utilizzato la crittografia simmetrica: si sfrutta la stessa chiave per cifrare e per decifrare un messaggio. È il caso di una cifratura del tipo Cesare (cioè le lettere del testo vengono spostate, per esempio la A diventa B, la B diventa C e così via). Si tratta della forma più semplice e comune di cifratura, molti algoritmi di crittografia di uso comune sono “semplici” (per esempio quello degli archivi Zip o Rar). Questo tipo di cifratura ha un grosso svantaggio: visto che la chiave necessaria per decifrare un messaggio è la stessa usata per criptarlo, è fondamentale che il mittente invii al destinatario anche la chiave, oltre al testo cifrato. E questo complica le cose, perché se era davvero necessario proteggere il messaggio con la crittografia, non si può certo spedire la chiave senza alcuna misura di sicurezza: se qualcuno intercetta la posta, potrebbe ottenere sia il testo che la chiave, risalendo quindi al contenuto originale in chiaro (cioè non cifrato). Una soluzione al problema della distribuzione della chiave è dato dalla crittografia asimmetrica, nella quale la chiave usata per cifrare e quella necessaria a decifrare il messaggio sono diverse. Tale meccanismo era stato ipotizzato dai crittografi Diffie, Hellman, e Merkle, ed è stato reso possibile dall’algoritmo sviluppato dai matematici Rivest, Shamir, Adleman (che è per l’appunto chiamato algoritmo RSA). Come è possibile avere due chiavi differenti per cifrare e decifrare un messaggio? In realtà è piuttosto semplice, lavorando con l’aritmetica dei moduli: per capirlo meglio, vediamo come funziona l’algoritmo RSA.
Per poter utilizzare questa cifratura abbiamo innanzitutto bisogno di due numeri primi, che chiameremo p e q. In teoria, questi dovrebbero essere molto grandi (altrimenti sarebbe troppo facile riuscire a scoprirli). Ci serve, poi un altro numero primo, più piccolo degli altri due: lo chiameremo e. Adesso possiamo calcolare il numero N come un semplice prodotto tra p e q. La chiave pubblica sarà data semplicemente dalla coppia N ed e. Quella privata, invece, si basa numeri N e d. Qui c’è un piccolo problema: il numero d si deve calcolare in modo tale che
(e*d) mod ((p-1)*(q-1)) = 1
possiamo, per semplificare, chiamare
(p-1)*(q-1) = phi
La relazione da soddisfare per ottenere d deve quindi essere:
(e*d) mod (phi) = 1
La cosa migliore per trovare d è andare per tentativi finchè non si identifica un numero in grado di soddisfare l’equazione. L’operazione “mod” è quella di modulo (cioè il resto della divisione). Per esempio,
7 mod 5 = 2
Poichè 7 diviso 5 fa 1 con il resto di 2. Ovviamente, d non dovrà mai essere rivelato perchè serve a decifrare i messaggi cifrati con e.
Come si può capire, il punto debole della crittografia RSA sta nel fatto di basare la propria sicurezza sulla difficoltà di scomporre il numero N in fattori primi e quindi risalire a p e q. Il problema è che la potenza dei computer aumenta ogni anno, e con essa la loro velocità nel fattorizzare un numero. Per tale motivo si cerca continuamente di costruire chiavi sempre più grandi: è una sorta di grande corsa contro il tempo in cui, per ora, i “buoni” sono avvantaggiati rispetto ai “cattivi”. Ma è probabile che entro qualche decina di anni la tendenza sarà invertita, e ci resterà solo la crittografia a blocco monouso come strumento per proteggere la privacy. Ad ogni modo, per cifrare usiamo (per ogni lettera) questa relazione:
C = T^e mod N
e per decifrare quest’altra:
T = C^d mod N
Dove C è il testo cifrato e T quello in chiaro.

Dai messaggi alle monete

Ora che abbiamo capito come funziona la crittografia asimmetrica per i messaggi, sarà facile comprendere il meccanismo su cui si basa Bitcoin. La rete Bitcoin è costruita come una rete P2P (come Kadmilla, per esempio). Ogni utente della rete ha diverse (potenzialmente illimitate) coppie di chiavi, che può raccogliere in un portafoglio digitale. In ciascuna di queste coppie, la chiave pubblica è resa nota a tutti e funziona da punto di invio o di ricezione per i vari pagamenti: è in un certo senso un po’ come un IBAN. Per tale motivo la chiave pubblica, che per essere precisi è costituita da 33 caratteri (scelti tra lettere e numeri), viene chiamata indirizzo bitcoin. Invece, la chiave privata corrispondente è nota esclusivamente al suo proprietario e serve a consentire il pagamento (cioè la cessione, non la riscossione). In questo modo, solo il proprietario della coppia di chiavi può davvero autorizzare la cessione di alcune sue monete Bitcoin. Un Bitcoin viene “creato” come ricompensa per il calcolo di un blocco (vedremo tra poco che significa) ed è una stringa di testo, contenente l’indirizzo del proprietario, cifrata con la chiave privata del proprietario stesso.
In seguito, se il proprietario vorrà cedere la sua moneta a qualcun altro per eseguire un acquisto, dovrà aggiungere ad essa l’indirizzo (la chiave pubblica) del nuovo proprietario e firmare il tutto con la propria chiave privata. Il fatto che si debba cifrare con la propria chiave privata fa sì che solo l’attuale proprietario possa porre la firma necessaria a concludere l’acquisto. Ciò significa che è sempre possibile risalire alla storia di una moneta: tramite l’ultima chiave pubblica è possibile decifrare la parte criptata. Questa è costituita da due parti: un’altra chiave pubblica e un altro “blob” criptato (da decifrare con l’indirizzo bitcoin appena citato). A sua volta, questo blob contiene un ulteriore indirizzo bitcoin e relativo blocco di testo criptato con esso. È quindi possibile proseguire fino alla stringa di testo originale, ricostruendo l’intera storia della moneta dal suo ultimo acquirente fino al creatore ottenendo tutti i vari indirizzi bitcoin attraverso cui la moneta in questione è passata.

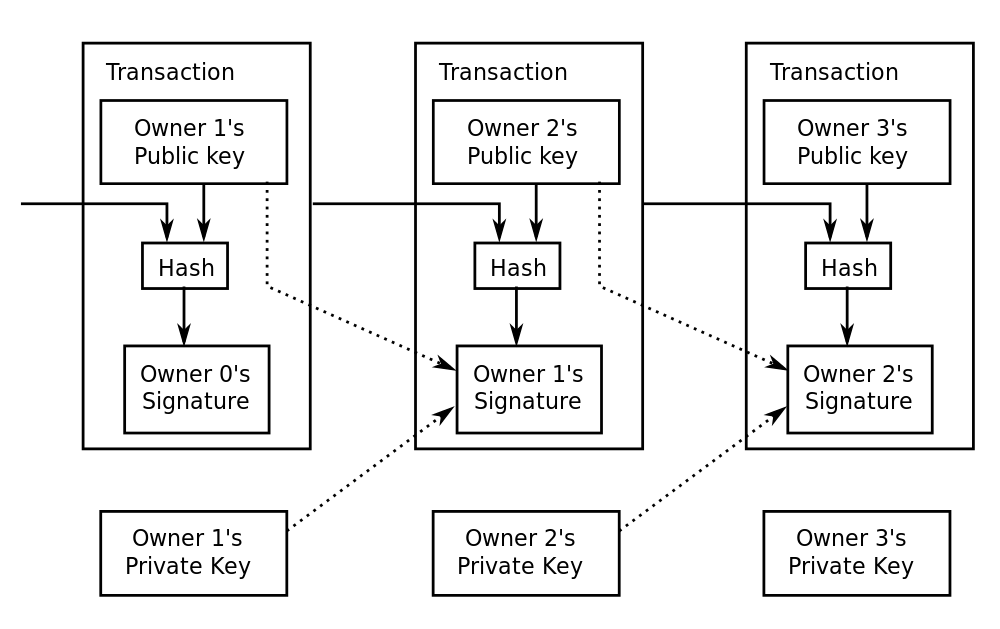
In pratica, ogni moneta Bitcoin esiste in quanto oggetto di una transazione economica: è addirittura costruita dall’insieme dei vari indirizzi che l’hanno posseduta. In fondo, ciò che conta di una moneta è poter eseguire delle transizioni: sono proprio queste il punto focale del meccanismo, quindi incentrare su queste il protocollo Bitcoin è la soluzione più semplice. Le transizioni sono pubbliche, anzi: quando si esegue un pagamento, le informazioni sulle monete (quantità di Bitcoin spesi, indirizzo del mittente e del destinatario) vengono inviate all’intera rete. Inoltre ogni client Bitcoin, per poter funzionare, deve scaricare dalla rete gli aggiornamenti in tempo reale sulle transizioni eseguite nel mondo. In questo modo è impossibile che un utente spenda due volte una propria moneta: quando esegue la prima transazione, tutti sanno che quel particolare Bitcoin è passato ad un altro utente e dunque non è più di sua proprietà.

Ma è davvero sicuro?

Si potrebbe obiettare che se davvero è possibile conoscere tutti gli indirizzi proprietari di una moneta, e tutti conoscono tutte le monete esistenti (grazie al database di informazioni), il sistema sia tracciabile. In realtà, però, gli indirizzi bitcoin vengono generati in modo casuale, e non possono essere collegati direttamente ad una persona: è infatti consigliabile utilizzare un indirizzo diverso per ogni transazione. Facciamo un esempio: se vogliamo permettere ai lettori del nostro blog di inviarci un pagamento tramite bitcoin, dovremo fornire pubblicamente un indirizzo a cui far arrivare i pagamenti. Ciò significa che tutti, Guardia di Finanza e Polizia Postale incluse saranno in grado di conoscere questo indirizzo ed i suoi movimenti, compresi e soprattutto quelli futuri: potrebbero facilmente scoprire quali oggetti servizi acquisteremo con quelle monete. La soluzione consiste nell’avere a disposizione diversi indirizzi bitcoin ma non dirlo a nessuno. Dal momento che le chiavi pubbliche non si possono collegare alle persone in modo automatico, ma solamente se il proprietario decidere di farlo sapere a tutti, è sufficiente avere un indirizzo “pubblico”, a cui tutti possono inviare denaro, e diversi indirizzi “privati”su cui trasferire le monete che arrivano a quello pubblico. In questo modo, eventuali inquirenti potrebbero sapere quante monete ci sono state cedute, ed anche quante ne abbiamo inviate ad altri indirizzi Bitcoin. Ma non potrebbero in alcun modo sapere chi sia il reale proprietario di questi indirizzi di arrivo: certo, potrebbero sospettare che si tratti di indirizzi che appartengono comunque a noi e che sia tutta una messa in scena per far perdere le tracce, ma non potrebbero dimostrarlo. Va anche detto che in realtà la “cronologia” di una moneta si può ricostruire solo grazie al database delle transazione, e non direttamente dalla moneta stessa. Questo perchè, di norma, invece di cifrare l’intero testo che costituisce la moneta per eseguire la firma che garantisce una transazione economica, si cifra soltanto un hash (con algoritmo SHA-2) del testo in questione. Un hash è un’altra stringa di testo ottenuta con una funzione di hash dalla stringa che rappresenta la moneta. La funzione di hash è per definizione non iniettiva, quindi non è biettiva e non si può invertire. Di conseguenza, dalla moneta si ottiene l’hash, ma dall’hash non si può ottenere la moneta. Tuttavia, ogni moneta realizza un unico hash, e questo può essere realizzato da una solo moneta: due stringhe di testo, cioè due monete bitcoin, differenti non possono generare lo stesso hash. Ciò significa che chi possiede una moneta può risalire fino all’hash generato dal suo precedente proprietario, ma lì deve fermarsi: non può ricostruire il contenuto della moneta prima che questa arrivasse nelle mani della persona da cui gli stesso l’ha ottenuta. Certo, può comunque risalire all’intera cronologia senza nemmeno bisogno di avere la moneta “in mano”: gli basta controllare il database comune delle varie transazioni.

Come si producono

L’ultima cosa che dobbiamo ancora scoprire sui Bitcoin è in che modo si possono ottenere. In fondo, per ogni moneta è fondamentale stabilire in che modo possa essere prodotta, per indicare anche un limite di produzione (anche nella realtà, la banca centrale europea non può stampare tutti gli euro che vuole, ci sono delle regole da rispettare).
Di solito nessuno si preoccupa di come vengano creati i bitcoin, perché esistono già strumenti in grado di farlo. Il fatto è che per degli sviluppatori è fondamentale saperlo, soprattutto perché man mano che passa il tempo servono sistemi sempre più efficienti per produrre nuovi blocchi, e quindi è necessario che qualcuno sappia come programmare questi “generatori di blocchi”.
Cos’è un blocco? Abbiamo detto che tutte le transizioni vengono comunicate, sottoforma di messaggio, all’intera rete Bitcoin. E la rete memorizza questi messaggi in diversi “blocchi”, che sono quindi semplicemente dei contenitori realizzati periodicamente.
Questo permette a nuovi client di scaricare facilmente l’intero elenco delle transizioni mai eseguite: basta ottenere tutti i blocchi, che tra l’altro sono identificabili (ci sono i blocchi della settimana scorsa, quelli di due mesi fa, quelli di tre anni cinque mesi e tre giorni fa, eccetera).
I Bitcoin vengono forniti agli utenti come ricompensa per avere risolto un problema matematico, operazione chiamata “mining” (letteralmente “scavare in miniera”). Il problema in questione consiste nell’identificare un numero (chiamato nonce) tale che dopo essere stato sottoposto due volte all’algoritmo di hash SHA-2 si ottenga una stringa che inizia con un certo numero di zeri. Naturalmente, visto che la funzione hash non è invertibile, si deve procedere per tentativi (un po’ come nel caso del brute force). Il numero di zeri che devono essere presenti all’inizio della stringa viene variato automaticamente per rendere l’operazione più semplice o più complessa in modo che venga sempre generato, in media, un nuovo blocco ogni 10 minuti. La difficoltà di trovare il numero nonce aumenta esponenzialmente con la quantità di zeri che devono essere presenti all’inizio della stringa ottenuta con il doppio hash.
Ogni nodo della rete, rappresentato da un utente con il proprio client, si occupa quindi di calcolare questo numero ed utilizzarlo per ottenere assieme al contenuto del blocco su cui sta lavorando un hash. Quando riesce ad ottenere l’hash che inizia con il giusto numero di zeri, comunica l’avvenuta scoperta a tutta le rete. Quando gli altri nodi della rete riconoscono che la soluzione proposta è corretta, “archiviano” il blocco, che entra dunque a far parte del passato, e cominciano ad inserire le prossime transizioni che riceveranno in un blocco completamente nuovo. L’insieme in ordine cronologico dei vari blocchi è chiamato “catena dei blocchi”. In pratica, la rete Bitcoin si comporta in questo modo:

• Quando due utenti eseguono una transazione, questa viene comunicata a tutti i nodi
• Ogni nodo minatore raccoglie le nuove transizioni di cui viene informato in un blocco
• Ogni minatore calcola la funzione per risolvere il problema matematico (questo è il mining vero e proprio)
• Quando un nodo trova la soluzione, cioè il numero nonce, la invia a tutto il resto della rete
• I nodi accettano il blocco soltanto se le transizioni in esso contenute sono valide
• Il minatore ottiene una ricompensa in bitcoin per il blocco contenente la soluzione che ha appena scoperto
• I nodi dichiarano di avere accettato il blocco ricevuto e cominciano a lavorare su un altro blocco utilizzando l’hash del blocco appena accettato.
• Si ricomincia da capo

Per ogni blocco vengono forniti dei Bitcoin, in numero decrescente nel tempo. Infatti, nel 2008 per ogni blocco venivano forniti 50 Bitcoin, mentre dal 2012 ne vengono prodotti 25 (e così sarà fino al 2016). La ricompensa verrà dimezzata ogni 4 anni fino ad arrivare a zero: secondo questo meccanismo, sarà possibile generare al massimo 21 milioni di monete. Visto che la complessità di calcolo aumenta sempre più, è oggi praticamente impossibile ottenere qualcosa con il proprio computer: è necessario utilizzare dei minicomputer dedicati (per esempio ASIC) oppure collaborare con altri minatori (per esempio tramite il sito www.bitminter.com). Nel caso della collaborazione, il sito si occupa di distribuire i bitcoin tra i vari utenti che hanno contribuito a risolvere il problema sul blocco. Ovviamente, visto che vengono forniti solo 25 Bitcoin e probabilmente ci sono ben più di 25 collaboratori tra cui distribuirli, ogni utente otterrà una frazione di moneta. In pratica, invece di ottenere 1 Bitcoin, riceverà 0,00X Bitcoin. Questo non è un problema, sia perché i Bitcoin possono essere divisi fino all’ottava cifra decimale, sia perché il valore dei Bitcoin può aumentare man mano che la gente li richiede.

Vendere online in Bitcoin

Per accettare pagamenti in Bitcoin sul proprio sito, è possibile sfruttare diversi servizi, come accept-bitcoin, che di fatto sono il PayPal per Bitcoin. Basta aggiungere al proprio sito un codice di questo tipo:

Nell’esempio stiamo vendendo 1Kg di Nduja per l’equivalente in Bitcoin di 20 euro. C’è anche una procedura guidata per realizzare questo codice, la si trova sul sito https://accept-bitcoin.net/bitcoin-payment-button.php. Ovviamente, pubblicare sul proprio sito web del materiale da pagare con Bitcoin ha poco senso: si viene facilmente tracciati. Molto meglio realizzare il proprio sito nel Dark Web, con Tor. Il bello di avere un server web che funziona sulla rete Tor, cioè un cosiddetto sito web Onion, è che non siamo identificabili: gli utenti del nostro sito web non possono risalire al nostro indirizzo IP reale, e quindi non ci possono identificare. Allo stesso modo, nessuno (noi compresi) può identificare gli utenti del nostro sito: tutti sono assolutamente anonimi.

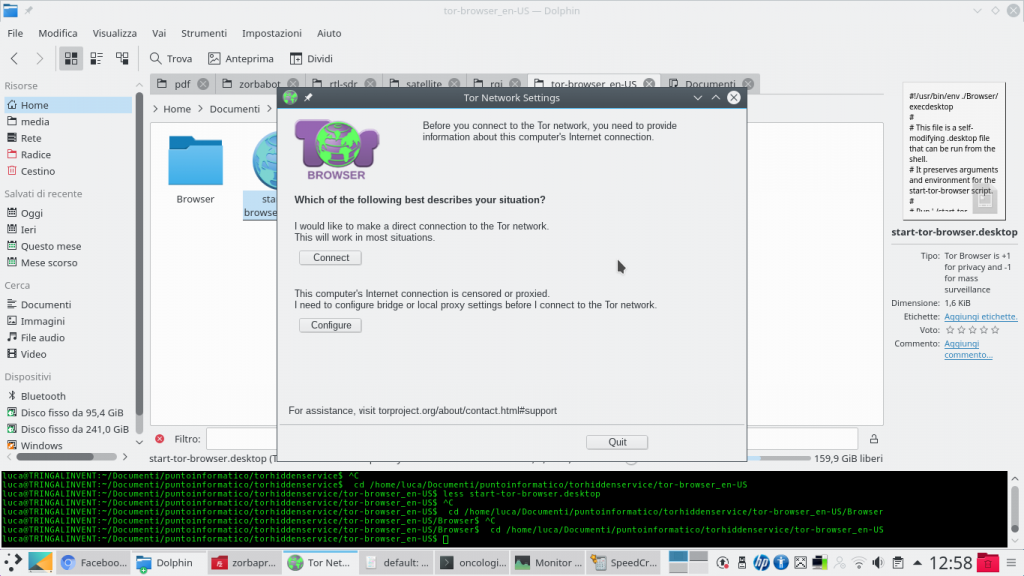
Quando si scarica Tor Browser, la prima finestra che appare permette di configurare la connessione ad internet: nel caso ci si trovi dietro ad un proxy (come nelle reti aziendali), può essere necessario cliccare su Configure. Altrimenti, basta cliccare su Connect per iniziare la connessione a Tor. Il servizio Tor rimarrà attivo finché Tor Browser è aperto: se lo si chiude, anche la connessione a Tor viene terminata.

I siti web con dominio .onion sono per l’appunto anonimi e costituiscono il dark web, che è un sottoelemento del deep web. Il deep web più in generale rappresenta tutti quei siti non rintracciabili dai normali motori di ricerca, ma all’interno del deep web il dark web è statisticamente la parte più ampia e interessante (esistono comunque anche siti privati, che non sono accessibili da chiunque pur non essendo anonimi) e per questo i due termini sono spesso usati come sinonimi. Questo anonimato offerto dai server .onion può non essere particolarmente importante per un normale cittadino italiano, ma è fondamentale per chi si trova in paesi che limitano la libertà di stampa: un cittadino ucraino poteva (durante la rivoluzione) pubblicare un sito Tor con notizie sui crimini del governo, senza il rischio di essere scoperto ed arrestato. Per fare un altro esempio, la procedura di invio dei file da parte degli informatori a Wikileaks funzionava proprio usando un server web Tor.

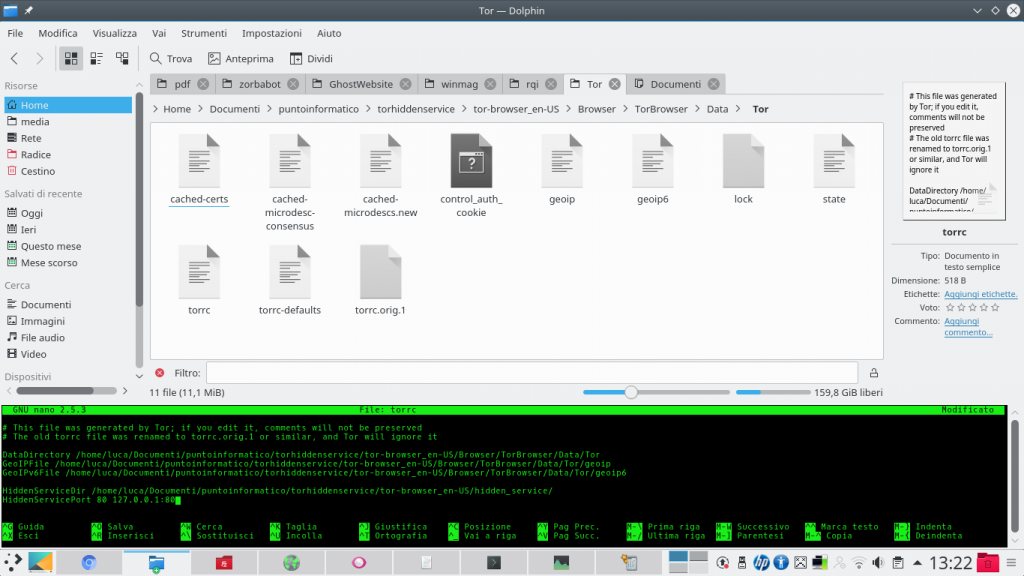
Per abilitare il proprio Hidden Service è necessario aprire il file che si trova nella cartella Browser/TorBrowser/Data/Tor/torrc con un editor di testo, e inserire alla fine di esso le righe https://pastebin.com/EEa4PegH. In questo modo si indica come server quello che viene ospitato sulla porta 80, e come cartella dei dati /home/luca/tor-browser_en-US/hidden_service/. Ovviamente, si può scegliere una cartella qualsiasi, e una qualsiasi porta (FTP funzionerebbe sulla porta 21).

Considerata la struttura della rete Tor stessa il client Tor può essere utilizzato sia per accedere a dei servizi che per proporre i propri servizi al resto della rete. Infatti Tor è un protocollo di Onion routing, un tipo di rete simile a una VPN, con una differenza importante: ci sono molti passaggi intermedi. Una VPN è di fatto una sorta di rete locale molto estesa sul territorio, tutti i computer si collegano a uno stesso server centrale che funziona come un router domestico e tiene assieme tutti i vari computer permettendo loro di condividere informazioni e un unico indirizzo IP pubblico. L’indirizzo IP pubblico è quello del server, quindi ogni client appare sul web con il suo indirizzo. Nell’Onion routing esistono molti passaggi intermedi: in pratica, un client si collega a un server, il quale si collega a un altro, poi un altro, e così via fino a un server finale che funziona come “punto di uscita” (un exit node). Il client apparirà sul web con l’indirizzo IP del punto di uscita, ma nessuno dei vari punti intermedi può risalire a chi sia il client e quale il nodo di uscita: ogni nodo intermedio della rete sa soltanto chi c’è prima di lui e chi dopo, ma non sa in che punto esatto della rete si trovi, quindi non sa se sta dialogando con il primo o l’ultimo computer della sequenza.

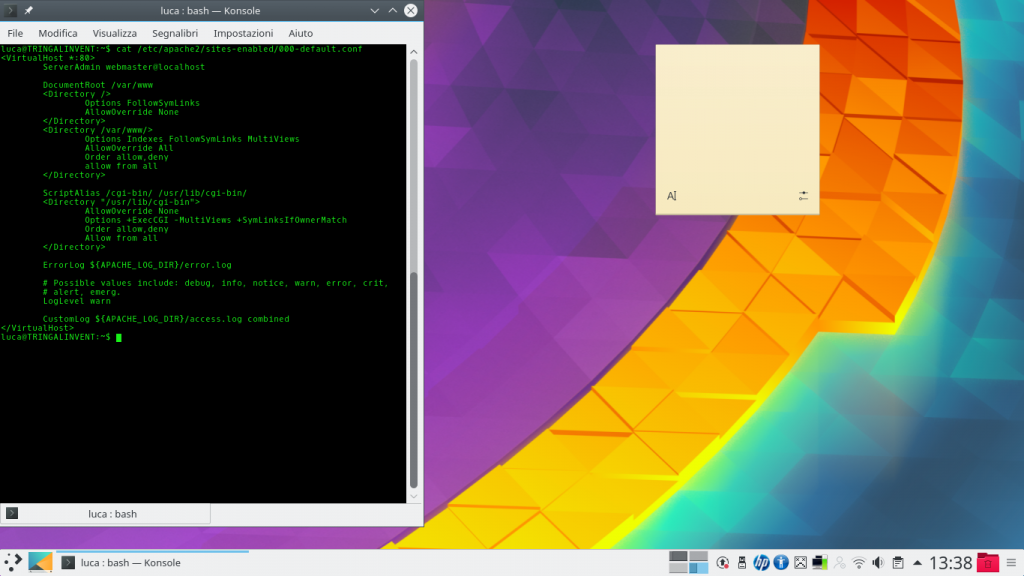
Ora è ovviamente necessario installare il server: se si vuole un server web, l’opzione probabilmente più scontata è Apache2, che può essere installato su sistemi Debian con il comando: sudo apt-get install apache2 php5 libapache2-mod-php5 php5-mcrypt Dando il comando cat /etc/apache2/sites-enabled/000-default.conf la riga DocumentRoot indica il percorso nel quale si possono inserire i vari file, per esempio la cartella /var/www/html/. Il file index.html dovrebbe già esistere.

L’idea ricorda un po’ le reti mesh, con la differenza che nelle reti mesh solitamente è possibile per tutti i computer essere punti di uscita per qualcun altro e non si può scegliere il proprio punto di uscita. Invece, nell’Onion routing i punti di uscita sono solo alcuni dei computer coinvolti, e un client può cambiare exit node se desidera apparire con un indirizzo IP differente da quello che ha avuto finora.
Inoltre, nell’Onion routing c’è un apposito sistema crittografico: un sistema a cipolla (il nome non è casuale, del resto). Ogni router intermedio si presenta al client con una chiave crittografica pubblica, che può essere usata per crittografare i pacchetti. Immaginiamo che un client riceva le chiavi di 4 diversi router: il client preparerà un pacchetto crittografandolo con la chiave 4, la chiave 3, la 2, e infine la numero 1. Il pacchetto verrà poi inviato ai vari router in sequenza, che lo potranno decifrare man mano: il primo router toglierà soltanto la crittografia con la propria chiave privata 1, il secondo con la chiave privata 2, eccetera. In questo modo, gli unici a poter vedere i dati non crittografati sono il client e l’exit node (e se si utilizza un protocollo come HTTPS nemmeno l’exit code può vedere i dati completamente decifrati, potrà farlo soltanto il vero destinatario). Le varie crittografie sono infatti applicate a strati come in una cipolla, e devono essere tolte esattamente in quell’ordine. Se qualcuno provasse a intromettersi il procedimento salterebbe e i dati diventerebbero automaticamente illeggibili, rendendo quindi tutta la comunicazione privata e di fatto anonima perché nessuno sa chi sia davvero ad avere cominciato la connessione.

Come si accede al server Onion

Per accedere ad un server Onion non si utilizza un indirizzo IP, ma un nome di dominio che viene creato in modo casuale sulla base di una altrettanto casuale e univoca chiave crittografica. Si tratta della chiave crittografica pubblica che permette ad altri client di crittografare, come abbiamo spiegato, i pacchetti di dati in modo che soltanto il nostro server sia in grado di leggerli usando la chiave privata di decifratura. Tutto quello che si deve fare per rendere il proprio client accessibile dalla rete Tor è selezionare le porte da “aprire” al resto del dark web (nel tutorial suggeriamo come fare per la porta 80).

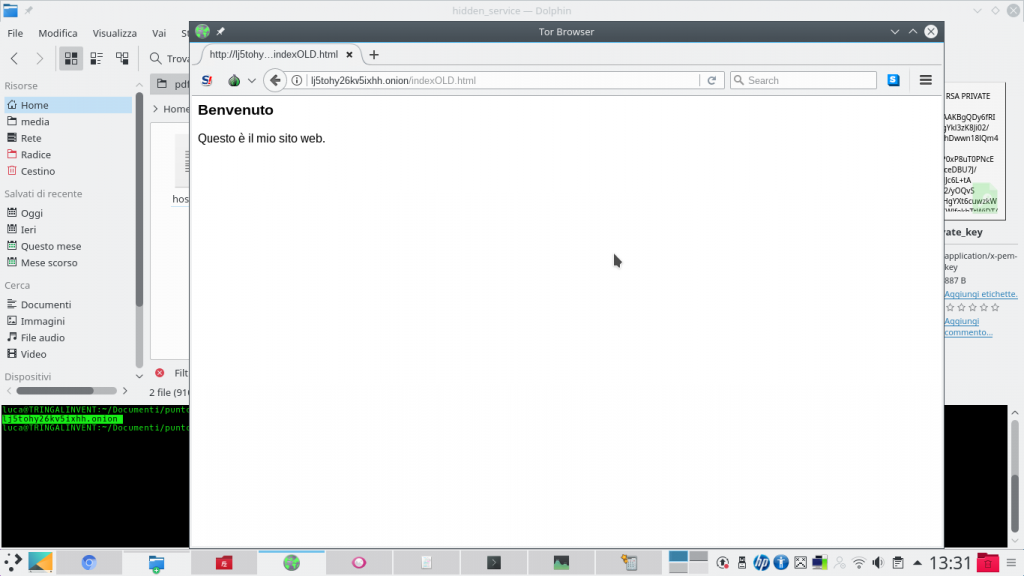
Per conoscere l’indirizzo del sito web sulla rete Onion, accessibile anonimamente tramite rete Tor, basta leggere il contenuto del file tor-browser_en-US/hidden_service/hostname. È l’indirizzo che si può condividere, anche sui motori di ricerca. Inserendo l’indirizzo su un Tor Browser è possibile visualizzare il sito appena creato. Per assicurarsi che il sito sia accessibile solo tramite rete Tor, e non sul web, è una buona idea chiudere la porta 80 sul proprio router.

C’è però una differenza importante con i server che si abilitano sul proprio computer per l’accesso dal web convenzionale: non si passa attraverso il meccanismo del NAT, perché il client Tor è già connesso direttamente alla rete Onion. Le normali reti locali casalinghe sono infatti gestite da un router, e sono quindi “nattate”: questo significa, in parole povere, che l’unico computer visibile direttamente da internet è il router stesso. Gli altri dispositivi della rete non sono normalmente visibili, e le loro porte di comunicazione (il server web utilizza la numero 80) sono chiuse. È quindi fondamentale, se vogliamo che il nostro server sia raggiungibile da internet, aprire la porta 80 del nostro computer. Questa procedura è detta “port forwarding”: se controlliamo il manuale del nostro router troveremo sicuramente una pagina in cui viene spiegato come eseguirla. Tuttavia, su rete Tor il server funziona anche se non abbiamo abilitato il port forwarding, perchè la connessione viene gestita direttamente dalla rete Onion. Anzi: è molto meglio non aprire la porta 80 sul router. Così, l’unico modo per accedere al server sarà tramite la rete Tor: un utente (e questo vale anche per i programmi di scansione automatica come Echelon o Prism) che si trova su internet (e che quindi può leggere il nostro vero indirizzo ip) non sarebbe in grado di entrare nel sito. Se aprissimo la porta sul nostro router casalingo, il nostro server diventerebbe accessibile dal web normale, non anonimo, e prima o poi qualcuno lo troverebbe (potrebbe finire sul motore di ricerca Shodan). Se la teniamo chiusa, l’unico modo per arrivare al nostro server web sarebbe proprio attraverso il client Tor che abbiamo attivo sul computer, quindi saremmo protetti dal meccanismo di anonimato.

Le ultime versioni di Tor Browser contengono Selfrando, sistema sviluppato dall’università di Padova per proteggere il programma dall’esecuzione remota di codice

Da quando sono esplosi gli scandali relativi all’uso dei dati dei social network, come quello di Cambridge Analytica, Facebook ha messo in piedi un sistema di controllo delle applicazioni. In poche parole, ora qualsiasi applicazione voglia accedere a ogni tipo di dato degli utenti deve prima superare un controllo in cui, in teoria, Facebook dovrebbe verificare che l’app non usi i dati in modo contrario alle norme di condotta previste dal social network.
Il problema è che, al momento, il sistema non funziona bene: ovviamente è appena partito, e si presume che in futuro verrà migliorato, ma ha una serie di difetti fondamentali che saranno difficili da correggere a meno che Facebook non sia pronto a spendere davvero molte risorse finanziarie. Già adesso, infatti, ci sono delle persone incaricate di analizzare ogni app che viene sottoposta alla verifica, ma hanno migliaia di app da seguire e non hanno quindi il tempo di entrare nei dettagli. Soprattutto, nessuno controlla il codice sorgente delle app, quindi non c’è davvero una garanzia che questo controllo serva a impedire utilizzi impropri dei dati del social network. Allo stesso tempo, inoltre, i meccanismi di autorizzazione delle app offerti al momento sono insufficienti a coprire alcune delle app più legittime: parliamo di quelle che collezionano dati pubblici per realizzare statistiche (per pubblica amministrazione, università, e ricerca). Al momento è molto difficile farsi approvare una app di tipo desktop, l’opzione non è prevista e gli script non sono visti di buon occhio. Tuttavia, una università, un istituto di statistica, o una redazione giornalistica hanno in genere bisogno di accedere soltanto a dati come i vari post delle pagine dei personaggi famosi (per analizzare il loro linguaggio e capire come cambi la comunicazione in caso di eventi importanti, o controllare la veridicità delle affermazioni). Un esempio semplice è un team di ricercatori che voglia controllare sistematicamente la percentuale di verità dei post di un politico, il cosiddetto fact checking. In questi casi si vuole accedere soltanto a dati che sono già pubblici, e che quindi possono essere raccolti senza violare la privacy di nessuno.

Abbiamo quindi pensato di realizzare uno script in Python che si occupi di eseguire lo scraping delle pagine Facebook pubbliche. Lo scraping è, per chi non lo sapesse, un insieme di tecniche di estrazione di informazioni da pagine web e altri documenti, in modo automatico, ripulendole da ciò che non serve. Un ricercatore universitario potrebbe scaricarsi i post di una pagina Facebook aprendola col browser e scorrendola verso il basso fino a visualizzarli tutti, selezionando il testo di ciascuno e copiandoselo. Ma sarebbe una operazione lunghissima e noiosa. Analizzando il codice delle pagine HTML che Facebook fornisce, invece, possiamo automatizzare l’estrazione dei testi (o delle immagini, se volete scaricarvi i meme delle vostre pagine preferite, basta modificare lo script per cercare i tag img invece dei tag p). E ovviamente lo script che realizziamo non richiede alcun accesso alle API o approvazione da parte di Facebook, perché di fatto faremo la stessa cosa che fa ogni utente che vuole guardare una pagina Facebook, permettendoci di bypassare tutte le verifiche che Facebook ha messo in piedi per le app.
Non dobbiamo, infatti, dimenticare un concetto fondamentale: se una informazione è disponibile, c’è sempre un modo non ufficiale per ottenerla. Quando carichiamo una pagina Facebook in Google Chrome, l’interfaccia realizzata con HTML e Javascript carica solo un certo numero di post. Quando “scrolliamo” la pagina, scendendo verso il basso, deve esserci una qualche funzione che si accorge che stiamo scendendo e quindi richiede al server un certo numero di nuovi post da visualizzare. È abbastanza ovvio che questa richiesta debba essere fatta, dalla pagina HTML+JS, con una richiesta HTTP (usando il meccanismo Ajax, quindi la funzione xmlhttprequest di Javascript). Se ne deduce che da qualche parte all’interno della pagina ci deve essere un riferimento a un’altra pagina che fornisce un elenco di post da visualizzare. L’accesso a questi dati da parte di script automatici invece che dai normali browser web è una cosa che, a prescindere dai suoi sforzi, Facebook non potrà mai impedire.

Scoprire l’indirizzo per ottenere i post

Per prima cosa dobbiamo scoprire come funzioni Facebook, cioè come vengano recuperati i vari post. In poche parole, bisogna conoscere il proprio obiettivo. Siccome si tratta di un sito web, la cosa migliore da fare è aprire una pagina Facebook (per esempio https://it-it.facebook.com/chiesapastafarianaitaliana/) col proprio browser, come Google Chrome, cliccando poi col tasto destro sulla pagina per scegliere la voce Ispeziona.

Tra le varie schede disponibili, quella che serve per capire cosa succeda è quella chiamata Network: si occupa di presentare in tempo reale le varie richieste HTTP che vengono fatte. Siccome è ovvio che la pagina di Facebook, per caricare altri post, abbia bisogno di fare una richiesta al server di Facebook per ottenerli, è anche ovvio che apparirà qui. Tutto quello che dobbiamo fare a questo punto è scorrere la pagina verso il basso, per obbligarla a caricare altri post: nel pannello vedremo comparire una richiesta a una pagina chiamata page_reaction_units. Sembra proprio che abbiamo trovato ciò che ci interessava: le altre eventuali richieste sono tutte relative a file accessori, come le immagini.

L’indirizzo della pagina contiene una serie di informazioni importanti, in particolare l’ID della pagina, ed è l’unica richiesta di questo tipo. Possiamo leggere il suo intero URL cliccandoci sopra col tasto destro del mouse e scegliendo Copy link address. Aprendo il link, si può capire che forma abbia la risposta: è una sorta di array JSON, una lista di oggetti vari, tra i quali il codice HTML necessario a presentare i post che sono stati richiesti. Si può facilmente distinguere il testo dei post in mezzo a tutto il codice. Alcuni caratteri vengono codificati come Unicode, inclusi alcuni pezzi dei tag HTML, e c’è sempre l’escape per i simboli /, che appaiono come \/, quindi è importante ricordarsi di convertirli in caratteri veri e propri, per poterli riconoscere facilmente (per esempio, \u003C\/p> è in realtà

).

Guardando meglio la risposta di pages_reaction_units si scoprono alcune cose interessanti. Innanzitutto, tutti i post che si sono ottenuti vengono presentati tra il testo {“__html”: e il testo ]]}, quindi possiamo selezionarlo facilmente. Inoltre, ogni post è preceduto dalla sua data, in vari formati. In particolare, c’è la forma Unix Time, che è molto comoda da gestire ed è sempre identificata dalla dicitura data-utime, quindi potremo distinguere i vari post dividendo l’intero HTML in più pezzi dopo ogni occorrenza della parola data-utime. E non solo: si può anche capire come ottenere ulteriori post, facendo un’altra richiesta a questa stessa pagina. Se infatti cerchiamo pages_reaction_units all’interno della risposta possiamo notare che c’è l’intero indirizzo di una richiesta come quella che abbiamo appena inviato, ma contenente anche il blocco timeline_cursor, con i riferimenti della timeline di Facebook relativi ai prossimi post. Possiamo quindi facilmente estrarre questi riferimenti per confezionare la nostra prossima richiesta.

Ora, tutto quello che è rimasto da scoprire è come costruire l’indirizzo da contattare per ottenere i vari post: sappiamo che serve pages_reaction_units più una serie di argomenti (che vediamo nella richiesta estrapolata dal browser). Non tutti gli argomenti sono però necessari, e possiamo scoprire quali siano superflui semplicemente provando a cancellarli uno alla volta e vedendo in quali casi si ottiene comunque il risultato desiderato. Scopriamo quindi che l’indirizzo necessario è qualcosa del tipo: https://it-it.facebook.com/pages_reaction_units/more/?page_id=286796408016028&cursor={“timeline_cursor”: “timeline_unit:1:00000000001528624041:04611686018427387904: 09223372036854775793:04611686018427387904″,”timeline_section_cursor”:{},”has_next_page”:true}&surface=www_pages_home &unit_count=8&dpr=1&__user=0&__a=1. Di questo indirizzo, abbiamo capito che la timeline_unit può essere scoperta all’interno di una richiesta precedente, mentre per scoprire l’ID della pagina Facebook basta scorrere il codice HTML della pagina stessa (che si può vedere nel browser Chrome con il prefisso view-source:) e cercare proprio pages_reaction_units, e subito dopo la parola page_id. Giocando un po’ con unit_count scopriamo che per la prima richiesta possiamo ottenere fino a 300 post, mentre per tutte le successive (quelle in cui si specifica la timeline_unit) il massimo che si può chiedere è 8 post. Tutto il resto è solo un insieme di argomenti vari sempre uguali, che nel nostro programma potremo quindi memorizzare sotto forma di variabili. 

La procedura per scaricare tutti i post sarà quindi intuitiva: si accede alla pagina leggendo il suo codice HTML per scoprire l’ID. Con questo si forma il primo URL da contattare per ottenere gli ultimi post. All’interno della risposta si prendono i post dividendoli e salvandoli separatamente, e si cercano anche i riferimenti della timeline_unit per poter fare una nuova richiesta e ottenere altri post, più vecchi. Poi si ripetono continuamente gli ultimi passaggi, leggendo la risposta, salvando i post, costruendo il nuovo indirizzo, e facendo una nuova richiesta, finché Facebook non fornisce più alcun post (il che significa che siamo arrivati all’inizio della pagina e i post sono finiti). Ora dobbiamo tradurre questa idea in uno script Python.

Leggere le pagine web

Cominciamo lo script, tutto in un unico file che chiamiamo scrapefb.py:

L’inizio è dato dalla shebang (#!), che su sistemi Unix è utile per automatizzare l’avvio dello script trattandolo come un eseguibile. Poi si devono importare tutte le librerie necessarie: urllib permette di scaricare il contenuto degli URL, e socket permette di stabilire un timeout sulle connessioni per chiuderle se sono inattive. Per fare il parsing della pagina web, cioè per leggere il suo contenuto distinguendo i vari “pezzi”, utilizziamo le espressioni regolari con la libreria re. Abbiamo anche bisogno di lavorare con data e ora, e accedere a funzioni relative al sistema operativo (per lettura e scrittura dei file).

Definiamo uno user agent: si tratta di una semplice stringa di testo che ogni sito richiede a chi vuole ricevere le pagine web, per capire di chi si tratti. Siccome possiamo scriverla come vogliamo, nessuno controlla davvero che stiamo dicendo la verità, possiamo scriverla in modo da convincere Facebook che il nostro script è in realtà il browser web Mozilla Firefox.

Definiamo una funzione che ci aiuti a scaricare tutto il contenuto di una pagina web, e la chiamiamo geturl. Prima di tutto, specifichiamo che ci serve lo useragent che abbiamo dichiarato nella sezione globale dello script. Poi ci assicuriamo di non procedere se l’url fornito alla funzione è vuoto, così evitiamo errori inutili. Costruiamo la richiesta HTTP utilizzando l’url. Servono anche un array di dati, che però in questo caso non è necessario visto che non abbiamo un form HTML da fornire alla pagina, e una intestazione. L’intestazione viene costruita con lo user agent, così Facebook ci scambierà per un browser web e non bloccherà la richiesta.

La richiesta HTTP può essere inviata usando la famosa funzione urlopen, e impostiamo anche un timeout. Il timeout è utile per non rimanere bloccati in eterno nel caso la connessione dovesse essere troppo lenta. Con un tempo di 300 secondi, sappiamo che al massimo dopo 5 minuti la situazione verrà sbloccata. La risposta del server alla nostra richiesta può essere letta con la funzione read, e nel caso qualcosa non abbia funzionato impostiamo la risposta (variabile ft) come vuota.

In teoria potremmo tenere la risposta così com’è, ma non è una buona idea: il web è una giungla di codifiche, e se non gestiamo la cosa rischiamo di ottenere testi illeggibili. Soprattutto per Facebook, che spesso codifica le varie emoticon sotto forma di caratteri speciali Unicode. Cerchiamo quindi prima di tutto di capire se il server ci suggerisca la codifica della pagina che ci sta inviando. In caso negativo, proviamo a decodificare il testo con la classica codepage di Windows 1252, uno standard sui sistemi Microsoft precedenti a Windows 10. Se non dovesse funzionare, proviamo a decodificare tutti i caratteri usando l’utf-8 togliendo però gli slash inutili (che spesso i server web forniscono per facilitare i browser), e altrimenti cerchiamo di tradurre direttamente l’intera pagina in una stringa python. Comunque sia andata, quindi, avremo una più o meno corretta stringa python piena di tutto il codice html della pagina. Per leggere meglio il suo contenuto, utilizziamo la funzione html.unescape per decodificare anche le varie entità dell’html (per esempio, &gt e &lt sono rispettivamente > e <, preziosi per interpretare il codice). L'unescape delle entità html non è fondamentale, ma rende il nostro lavoro più comodo.

Cercare l’ID della pagina Facebook

Cominciamo a scrivere la funzione vera e propria per lo scraping delle pagine di Facebook. La funzione richiede, come argomenti, l’indirizzo della pagina da scaricare, la cartella in cui salvare il risultato, e se si debba salvare il risultato come tabella CSV invece che come testo TXT.

Innanzitutto ci sono un paio di informazioni, che possiamo memorizzare in alcune variabili. Potremmo anche scriverle direttamente nelle funzioni che le usano, come vedremo, ma tenendole nelle variabili è molto più facile modificarle in futuro se dovesse essere necessario a causa di modifiche nel funzionamento di Facebook. La variabile TOSELECT_FB contiene la stringa da cercare dentro la pagina Facebook per conoscere l’URL che fornisce i vari post. Le due successive variabili sono le stringhe che delimitano l’inizio e la fine dei post nella risposta. Infatti, Facebook non fornisce solo l’elenco dei post della pagina, ma anche una serie di altre informazioni che non ci servono. Per non complicarsi la vita, bisogna avere un output pulito, quindi toglieremo tutto ciò che non ci serve isolando solo il testo presente tra quei due delimitatori. Stabiliamo poi il numero di risultati che vogliamo: il massimo consentito da Facebook (al momento) per la prima richiesta è di 300 post. Inoltre, specifichiamo un periodo di attesa prima di inviare le richieste successive, per evitare che il server possa accorgersi che ne stiamo facendo troppe tutte assieme. Le ultime due rappresentano l’inizio e la fine del link per ottenere i vari post: vedremo tra un po’ come costruirlo nella sua interezza.

In questo momento siamo pronti per eseguire la prima richiesta e scaricare la pagina Facebook. L’indirizzo che contattiamo è qualcosa del tipo https://it-it.facebook.com/chiesapastafarianaitaliana/. Ovviamente otteniamo soltanto gli ultimi post, proprio quello che un utente normale vede quando carica la pagina. Di per se i post che appaiono non ci interessano, li otterremo contattando direttamente l’URL che fornisce tutti i post. Il codice HTML di questa pagina ci interessa soltanto perché possiamo estrarre delle informazioni. In particolare, vogliamo scoprire il dominio di Facebook, cioè tutto quello che è compreso tra https:// e il primo / successivo. Nel caso in esempio è it-it.facebook.com, ovviamente è diverso per ogni paese (una pagina spagnola non inizierà con it-it). Cerchiamo anche di capire il nome della pagina, che è tutto ciò che segue il dominio: siccome lo useremo come nome del file in cui salvare i risultati è fondamentale che non ci siano caratteri strani. Usando una espressione regolare, cancelliamo (sostituiamo con “”) tutti i caratteri che non siano lettere o numeri. Fondamentale per poter proseguire è il pageid, cioè il numero identificativo della pagina che vogliamo scaricare: questa informazione si può recuperare dalla pagina stessa perché è sempre presente in essa un link che contiene tale numero. Il link in questione ha la forma ?page_id=286796408016028&cursor, quindi possiamo scoprire l’ID cercando ciò che segue la parola page_id= e arriva fino al simbolo &. Ci si potrebbe chiedere come mai per cercare i vari delimitatori utilizziamo direttamente la funzione index, molto pratica e veloce, mentre per cercare la posizione del ‘pages_reaction_units’, che determina l’inizio del link in cui troviamo la pageid, usiamo le RegEx. La risposta è semplice: per ora trovare questa stringa è facile, ma in futuro potrebbe essere necessario usare una espressione regolare. In questo modo, lo script è già pronto per future modifiche.

Ora che abbiamo tutte le informazioni necessarie, possiamo costruire il nome del file in cui andremo a scrivere i post recuperati. Il nome è dato dalla cartella in cui salvare i file più fb_ e il nome della pagina. Ovviamente, se l’utente vuole un TXT l’estensione del file sarà TXT, e se vuole un CSV l’estensione sarà CSV. Creiamo anche un altro file, con stesso nome la estensione .tmp. Questo è il file in cui andremo ad inserire i vari link già visitati, così se si deve riprendere lo scaricamento dei post di una pagina Facebook non lo si ricomincia da capo ogni volta, ma si riprende da dove ci si era interrotti. Per l’appunto, nel caso il file esista già vuol dire che non si deve ricominciare da capo, quindi si carica l’intero contenuto del file in una lista, chiamata alllinks. In questa lista ogni elemento è un link, perché il file è stato diviso riga per riga (e quando lo scriveremo, metteremo un link in ogni riga). Definiamo anche una variabile che faccia da contatore, per sapere quante richieste di post siano state fatte, e una che stabilisca se stiamo ripristinando un download interrotto o se dobbiamo ricominciare da capo.

Richiedere i post della pagina al server di Facebook

Siamo al momento della raccolta vera e propria dei post della pagina. Siccome dobbiamo fare tante richieste una dopo l’altra, utilizziamo un ciclo. Il ciclo while andrà avanti finché la variabile active sarà True. Ne consegue che per fermare il ciclo, se necessario, non dovremo fare altro che porre tale variabile uguale a False. 

Il link viene costruito unendo il dominio di Facebook, la parte iniziale del link, l’id della pagina, e la parte finale. Sarà quindi qualcosa del tipo https://it-it.facebook.com/pages_reaction_units/more/?page_id=286796408016028&cursor={“card_id”:”videos”,”has_next_page”:true} &surface=www_pages_home&unit_count=300&referrer&dpr=1&__user=0&__a=1, come si può notare ci sono tutti i vari pezzi che abbiamo costruito finora. Se provate ad aprire questo indirizzo col browser vi accorgerete che fornisce una serie di informazioni, tra cui l’html dei vari post che sono stati richiesti (cioè gli ultimi 300 post della pagina). Inseriamo il link appena costruito nel file che li deve memorizzare, così se lo script dovesse bloccarsi mentre cercare di recuperare i post sapremo di dover ricominciare da questo preciso link, e non doverli rifare tutti da capo. Usando la modalità di accesso al file “a” eseguiamo un “append”, cioè inseriamo direttamente questo link alla fine del file, in una nuova riga, senza bisogno di preoccuparci di quali altri link ci fossero prima (non dobbiamo quindi aprire il file, leggerlo, aggiungere il nuovo link, e poi salvarlo). È un risparmio di risorse importante.

Sempre utilizzando la funzione geturl possiamo recuperare anche con il nostro script tutta la risposta del server di Facebook. Siccome ci interessa soltanto la parte con i vari post che abbiamo richiesto, la estraiamo e la memorizziamo nella variabile postshtml. Il codice HTML dei vari post va un po’ ripulito: Facebook usa molti caratteri che non sono UTF-8 per gestire le emoticon, in genere sono utf-16. Però per il nostro scopo sono fastidiosi, le emoticon non ci interessano affatto e l’elaborazione dei testi è molto più facile con l’utf-8. Quindi ci assicuriamo di tradurre tutti i caratteri in UTF-8, togliendo anche l’escape dei caratteri speciali. Facebook, infatti, decide che alcuni caratteri sono particolari e li presenta con al loro notazione Unicode, una cosa del tipo \u0001. Questo è molto scomodo per noi, quindi forziamo la trasformazione in caratteri leggibili. A questo punto potrebbero essere rimasti dei simboli che UTF-8 non è in grado di gestire, perché si tratta delle famigerate emoticon UTF-16. Si riconoscono perché il codice Unicode è compreso tra \uD800 e \uDFFF. Siccome non ci interessano, usiamo una semplice espressione regolare per cancellarli, sostituendoli con la stringa vuota “”. Ora abbiamo finalmente l’intero codice HTML dei post, pulito e pronto per essere letto e interpretato. Siccome ogni post di Facebook è contrassegnato da un orario nel formato Unix Time (uno standard di internet), possiamo spezzare il contenuto dell’HTML nei singoli post dividendo proprio in base a ‘data-utime’, che è la stringa che Facebook usa per indicare l’orario di un post.

In questo momento, la lista postsarray contiene i vari post: in realtà, il primo elemento della lista non contiene post, perché ha tutto l’HTML precedente. Comunque, possiamo scorrere la lista e individuare i post banalmente cercando il loro timestamp, cioè l’orario della pubblicazione. È facile da identificare, perché come dicevamo ogni post viene preceduto da una span (elemento HTML) che contiene una dicitura di questo tipo: data-utime=\”1531306802\” data-shorten=\”1\” class=\”_5ptz\”>. Siccome noi stiamo dividendo l’HTML a ogni “data-utime”, è ovvio che ogni post inizierà con=\”1531306802\” data-shorten=\”1\”…, e quindi l’orario in formato Unix sarà il primo numero tra virgolette (nell’esempio è 1531306802). Per essere sicuri di nona vere problemi, usiamo una RegEx per cancellare dal timestamp ottenuto qualsiasi cosa non sia un numero, e convertiamo il risultato in un int, cioè un numero intero. Nel caso non sia possibile risalire a questo numero, come per il primo elemento della lista che non è un vero post, consideriamo il numero pari a zero. Poi, usando datetime, possiamo convertire questo timestamp in una data facilmente leggibile, nel formato anno-mese-giorno ore:minuti:secondi. La data viene quindi aggiunta alla lista timearray, che abbiamo appositamente creato. Ciò significa che per ogni elemento di postsarray, cioè ogni post della pagina Facebook, abbiamo un corrispondente elemento di timearray, cioè la data della pubblicazione del post stesso.

Tutto il testo (se c’è) del post numero i si trova dentro all’elemento postsarray[i], ma è ovviamente circondato da un sacco di altri pezzi di HTML che non ci servono. Per estrapolare soltanto il testo dei post basta prelevare tutto ciò che si trova all’interno dei paragrafi (che nella risposta di Facebook sono i tag

<\/p>). Bisogna ricordare che nello scrivere l’espressione regolare per trovare i tag il carattere \ ha bisogno di una sequenza di escape lunga, e va scritto come \\\\. La funzione finditer crea l’array indexes, che contiene tutte le posizioni in cui si trovano i vari paragrafi: un post di Facebook può infatti essere diviso in tanti paragrafi, e noi li vogliamo tutti. Ciascun elemento di indexes, contiene in realtà due informazioni: la prima (cioè 0) è l’inizio del paragrafo, e la seconda (cioè 1) è la fine del paragrafo. Usando il classico sistema di slicing delle stringhe di Python, si può banalmente estrarre il testo di ogni paragrafo semplicemente partendo dal carattere iniziale e finale (quindi postsarray[i][start:end], perché la stringa è postsarray[i]). Alla fine del ciclo for che legge tutti i vari indexes, avremo la variabile thispost che contiene tutti i vari paragrafi uniti, senza gli altri tag inutili.

Possiamo assegnare tutto il testo del paragrafo all’elemento stesso da cui eravamo partiti, così lo avremo ripulito. Prima, però, togliamo i tag che ancora esistono. Per esempio, il grassetto viene realizzato con i tag , quindi noi cancelliamo tutto cioè che si trova tra i simboli < e >. E cancelliamo anche gli slash non necessari. Quindi, gatti\/cani diventa gatti/cani. Alla fine presentiamo l’array sul terminale, così è più facile fare il debug e capire se qualcosa non vada bene. Lo scraping è pur sempre legato a qualcosa di molto casuale, e può capitare che in situazioni particolari qualcosa improvvisamente non funzioni.